Gestelltes Problem
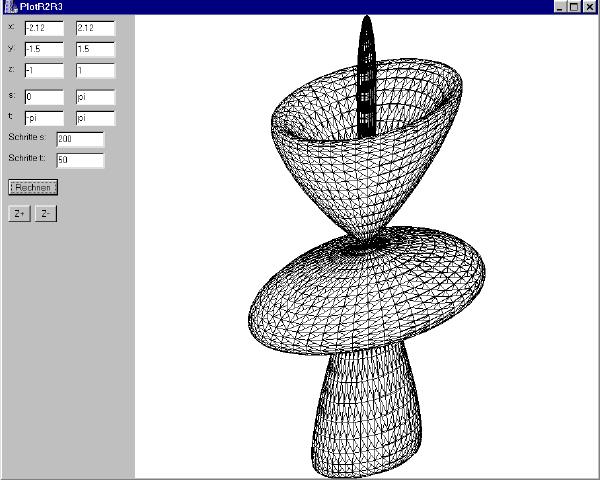
Da ich zum Ausmalen (siehe Computergrafik) gerne Bitmaps mit möglichst vielen Einzelflächen als Ausgangsbasis nehme, dachte ich daran, dass doch zur Abwechslung einmal 3-dimensionale Objekte interessant wären. Solche Programme hab’ ich schon früher geschrieben, allerdings in Turbo-Pascal, einer Sprache die damals auf IBM-kompatiblem PC’s mit MS-DOS wirklich unschlagbar war, den Sprung zu Windows aber nicht geschafft hat. Mitte der 80er war das für mich an der Uni als Darstellung von Elektronenorbitalen (Kugelfunktionen) eine Übungsaufgabe in theoretischer Physik. Entweder die Darstellung der Kugelfunktionen am PC oder eine “schriftliche Aufgabe”. Damals hab’ ich mich in drei Millisekunden für die Programmieraufgabe entschieden. Der Professor meinte dann übrigens zu meinen Ausdrucken “Das ist die beste Darstellung der Kugelfunktionen, die ich jemals gesehen habe. Wie haben Sie das gemacht?”
Es ging jetzt also darum, diese Darstellung in C++ zu implementieren.

Algorithmus
Die Koordinaten der Fläche werden durch drei Funktionen X(s,t), Y(s,t), Z(s,t) berechnet. Die Intervalle für s und t werden vom Benutzer gewählt, ebenso eine Anzahl Schritte, in die die Intervalle eingeteilt werden. Das Programm durchläuft das Intervall und ermittelt für je drei Punkte aus dem Intervall drei Punkte im Raum, die dann ein Dreieck ergeben. Diese Dreiecke werden in einer Liste abgelegt. Nach der Berechnung wird die Dreiecksliste so sortiert, dass die vom Betrachter am weitesten entfernten Flächen an den Anfang der Liste kommen. Dann wird die Liste gezeichnet, wobei jedes Dreieck mit der Hintergrundfarbe gefüllt wird. Dadurch verdecken die vorderen Flächen die hinteren.

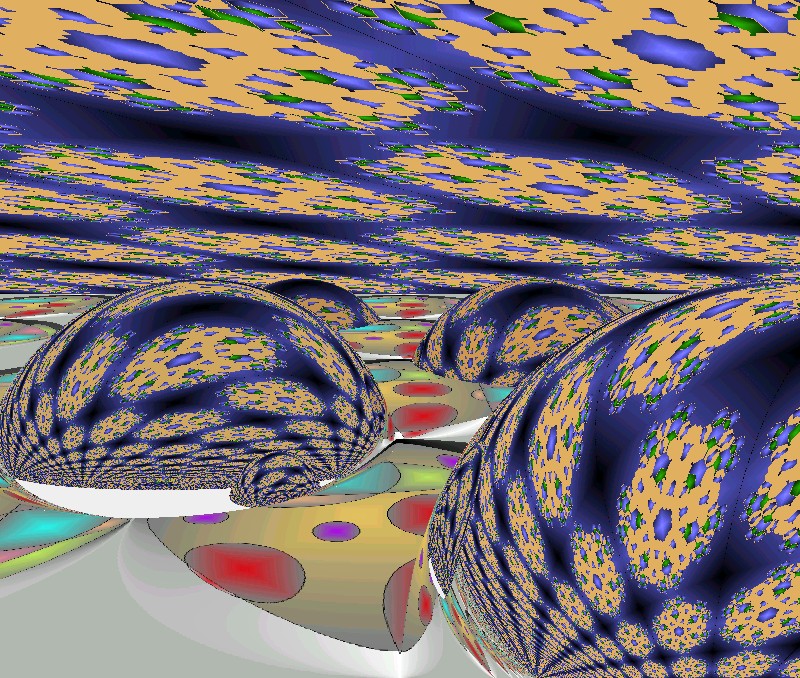
Screenshot (20.000 Flächen):

Gestelltes Problem
Hier eine Platte, da eine Platte, Datensicherungen vom Arbeits-PC. Diverse Rechnerwechsel. Irgendwann waren meine Datenbestände wirklich komplett durcheinander, alles mehrfach irgendwo abgelegt. Deshalb brauchte ich mal wieder ein Programm zum Auffinden von Duplikaten. Es sucht in einem Verzeichnisbaum rekursiv nach identischen Dateien. Die gefundenen Gruppen von Dateien gleichen Inhaltes werden dann in einem Tree-Control angezeigt und können gelöscht werden.

Algorithmus
Zunächst alle Dateien auffinden. Dabei prüfen, ob es Dateien mit identischer Länge gibt. Für diese eine Checksumme bilden. Dateien mit gleicher Länge und gleicher Checksumme werden gruppenweise verglichen. Es ergibt sich also eine Liste mit Gruppen von identischen Dateien.

Screenshot:

Gestelltes Problem
Meine Kumpels und ich digitalisieren unsere CDs. Wir tauschen nur zu Backupzwecken und völlig unkommerziell. Bei einer MP3-Sammlung stellt sich ab einer gewissen Grösse die Frage, ob man ein bestimmtes Lied nicht schon irgendwo hat. Manuelle Abgleiche sind zeitaufwendig.

Algorithmus
Das Programm scannt einen Verzeichnisbaum auf MP3-Dateien, liest diese ein, und erzeugt eine Informationsdatei mit einem Extrakt aus den ersten 15 Musiksekunden sowie anderen Dateiinformationen. Diese Dateien werden in einem zweiten Schritt wieder eingelesen und dem Anwender in Form einer Liste präsentiert. In dieser Liste werden Dateien mit gemeinsamen Merkmalen zusammengefasst. Die Liste wird zunächst sortiert und dann Dateien mit gemeinsamen Merkmalen markiert. Folgende Sortierkriterien sind bis jetzt implementiert:
Dateiname (ohne Verzeichnis), Dateiname “tolerant” (Ziffern und Sonderzeichen entfernt), Dateigrösse, Dateigrösse “tolerant” (Dateilängen, die sich um maximal 100 Byte unterscheiden, gelten als identisch), Bitrate der MP3-Datei (alles unter 160 kBit/s ist schlecht), Samplingfrequenz (normal 44 kHz) und die Position des Lautstärkemaximums der ersten 15 Musiksekunden.
Damit kann man schon viele Doppelte erkennen, trotzdem muss bei der Verarbeitung der eigentlichen Musikdaten noch etwas getan werden.

Screenshot:

Gestelltes Problem
An meinem Notebook sind zwei USB-Laufwerke angeschlossen. Auf dem Ersten befinden sich meine MP3-Dateien. Das Zweite wird zu Backupzwecken genutzt. Nun brauchte ich ein Programm, mit dem man zwei grosse Verzeichnisse mitsamt Unterverzeichnissen synchron halten kann. Mit dem Windows Explorer kam ich nämlich nicht weiter weil dieser beim Kopieren die schon vorhandenen Dateien erneut kopiert was bei grossen Dateianzahlen einfach zu lange dauert.

Algorithmus
Da ist nicht viel Algorithmus dabei, es wird ein Quellverzeichnis rekursiv durchsucht und geprüft, ob die dort liegenden Dateien im Zielverzeichnis mit gleicher Länge vorliegen. Falls nicht, werden sie kopiert. Nach dem Kopieren wird für jede Datei im Zielverzeichnisbaum geprüft, ob sie im Quellverzeichnisbaum vorhanden ist (sie könnte ja seit dem letzten Lauf gelöscht oder umbenannt worden sein). Falls sie dabei nicht gefunden wird, wird sie gelöscht.

Screenshot:

Gestelltes Problem
Angenommen, man hat ca. 10.000 Jpeg-Dateien unter denen sich viele Doppelte befinden. Diese Dubletten können sich in der Bildgrösse, in den Bildproportionen, der Helligkeit und auch der Farbverteilung unterscheiden.

Algorithmus
Das einfachste ist ein Vergleich der Dateigrössen. Damit hab’ ich viele Dubletten gefunden, aber natürlich meine Anforderungen noch nicht erfüllen können. Die eine Hälfte des Algorithmus ist dadurch aber schon entstanden und zwar ist das eine Sortierung und eine anschliessende Anzeige von Dateien mit gleichem “Kennwert”, zunächst eben der Dateigrösse. Ich habe mir den Quelltext für das Einlesen von Jpeg-Dateien von der “Independent JPEG Group” downgeloaded (wenn jemand mal erschreckend guten Quelltext sehen will, da ist er richtig) und somit Zugriff auf die Bilddaten. Zur Einbeziehung des Bildinhaltes werden die Jpeg-Dateien auf eine wahnsinnig schlechte Auflösung heruntergerechnet (8×8 Pixel). Dann werden sie in schwarz-weiss konvertiert, wobei ein Punkt dann schwarz ist, wenn er dunkler ist als die Durchschnittshelligkeit des Originalbildes, ansonsten weiss. Es ergibt sich also eine 64bit-Ganzzahl und nach diesem Wert werden die Bilder sortiert und dann Dateien mit gleichem Kennwert angezeigt. Dann kann der Anwender sich beide Versionen angucken und entscheiden ob die Bilder wirklich identisch sind.

Screenshot:

Gestelltes Problem
Ein Bekannter, Besitzer eines Kreditinstituts, hatte die Idee, die Börsenkurse bekannter Gesellschaften auf kurzperiodische Regelmässigkeiten (im Bereich einiger Tage) zu untersuchen. War es vielleicht so, dass es bei einer Aktie, die an einem Tag um 5% gestiegen war, für den nächsten Tag eine grössere Wahrscheinlichkeit gab, dass sie wieder steigen würde? Zur Analyse hatte er die Kursdaten einiger Aktien für die letzten 10 Jahre zusammengestellt.

Algorithmus
Ich verwarf zunächst den Ansatz, aus dem vorhandenen Datenbestand Regeln abzuleiten, da ich der Meinung war, dass eine Prognose für den Folgetag sich aus den Daten der vorhergehenden Tage unter direkter Einbeziehung der Datenbasis ergeben müsste.
Ich möchte den Algorithmus kurz an einem Beispiel demonstrieren. Geladen wurden die Kursdaten der Oracle-Aktie von 1993 bis 2002. Sie sind im oberen Fenster dargestellt. Die Pfeile geben die Kurstendenz wieder. Am 15.4.2002 ist die Aktie um 1,8% gefallen. Versetzen wir uns nun an diesen Tag zurück. Durch Klicken auf die entsprechende Zeile im oberen Fenster wird dieser Tag markiert, dann drücken wir auf Rechnen. Das Programm sucht sich nun die Daten vom aktuellen Tag, dem Vortag und dem Vorvortag zusammen, da eine Samplelänge von drei Tagen eingestellt ist. Es ergibt sich also dieses Sample: (-1,83/5,21/-5,28). Das Programm nimmt nun dieses Sample und legt es über die Kursdaten der letzten zehn Jahre und sucht dabei nach ähnlichen Samples. Diese werden absteigend nach der Ähnlichkeit sortiert und im unteren Fenster dargestellt. Das Sample mit der grössten Ähnlichkeit ist vom 22.2.2002. Damals ist der Kurs am nächsten Tag um 1,57% gestiegen. Das zweitähnlichste ist vom 14.6.1994, mit einem Anstieg von 1,42%. Beim drittähnlichsten Sample, der 16.2.2000 trat ein Verlust von 0,21% auf. Insgesamt sehen wir im unteren Fenster überwiegend Pfeile, die nach oben zeigen. Wenn wir uns also entscheiden die Aktie zu kaufen, dann würden wir am 16.4.2002 mit einem Gewinn von 6,74% belohnt werden. Über den Knopf “Spekulieren” kann der Auswahlvorgang automatisiert werden. Dabei wählt man ein Datum aus, welches z.B. ein Jahr in der Vergangenheit liegt. Das Programm erstellt dann für diesen Tag eine Prognose und entscheidet sich im positiven Fall, die Aktie zu kaufen. Dann prüft es, ob es Gewinn oder Verlust gemacht hätte und nimmt sich den Folgetag vor und entscheidet anhand einer erneuten Prognose, ob es die Aktie halten oder verkaufen soll und so weiter. Bei solchen Testspekulationen erzielt das Programm jährliche Profite im zweistelligen Prozentbereich. Es gibt also tatsächlich kurzperiodische Regelmässigkeiten in Aktienkursen. Trotzdem bin ich nicht reich geworden, da für den Kauf und den Verkauf einer Aktie jeweils Transaktionskosten anfallen. Da das Programm sehr viele Transaktionen macht, werden die Kursgewinne von den Transaktionskosten mehr als aufgefressen. Spass hats trotzdem gemacht.

Screenshot:

Gestelltes Problem
Brettspiele hab’ ich schon viele gemacht, das ist das erste was funktioniert (bis auf eine kleine Endspielschwäche beim Springen, aber normalerweise kommt man nicht so weit).

Algorithmus
Minimax-Alpha-Beta.

Screenshot:

Gestelltes Problem
Ursprünglich ging es um eine Wette mit einem Kumpel, wer wohl das bessere Programm für das Spiel Mastermind schreiben könne. Das Schwierige dabei war, dass der Computer die Kombination erraten musste. Ich habe fast zwei Wochen gebraucht, bis ich einen Algorithmus fand. Wer damals (1988) die Wette gewann wird nur per Mail verraten.
1997 habe ich dann das Programm in Java erneut geschrieben. Auch die Grafiken sind alle selbst gemacht.

Algorithmus
Ist eigentlich enttäuschend einfach. Es werden alle möglichen Kombinationen in einem Feld gespeichert. Die erste Kombination aus diesem Feld, im Screenshot (hier weiss, schwarz, blau, gelb) wird dem Benutzer angeboten. Dann gibt der Benutzer seine Bewertung (hier zwei weisse Stecker). Nun kommt der Trick. Das Programm nimmt jede Kombination aus dem Feld und prüft, welche Bewertung der Benutzer der eben angebotenen Kombination gegeben hätte, wenn es die Kombination des Benutzers wäre. Wenn der Benutzer also die Kombination (weiss, schwarz, blau, gelb) hätte, dann würde er für die angebotene Kombination (weiss, schwarz, blau, gelb) vier schwarze Stecker vergeben. Er vergab aber zwei weisse Stecker. Also wird diese Kombination gestrichen. Übrig bleiben die Kombinationen, die zusammen mit (weiss, schwarz, blau, gelb) zwei weisse Stecker ergeben. Jetzt wird die erste der übrigen Kombinationen (schwarz, weiss, grün, rot) angeboten. Nach maximal sechs Zügen ist die Kombination erraten.

Screenshot:

Gestelltes Problem
Anfang der Neunziger Jahre des letzten Jahrhunderts habe ich in der c’t einen Artikel über die Erzeugung perspektivischer Bilder mit dem Verfahren des Ray-Tracing gelesen. Daraufhin hab’ ich mich sofort an den Rechner gesetzt, denn ich wollte auch sowas machen.

Algorithmus
Das sprengt hier den Rahmen. Grundprinzip ist, dass man vom Auge des Betrachters aus durch jeden Bildpunkt einen “Lichtstrahl” schickt und ausrechnet, wohin dieser reflektiert wird. Die Farbe des getroffenen Punktes bestimmt dann die Farbe des Bildpunktes. Dafür braucht man jede Menge fiieeser Vektorrechnung. Es ist letzten Endes nicht trivial, auszurechnen wohin sich ein Strahl bewegt, der von einer Kugel reflektiert wird.

So sieht das dann aus:

Oder so: